取っ付きにくくても避けては通れない道
MACDがシグナル線を上抜いたら、終値が直近30本の高値を上抜いたら、陰線が3本連続で続いたら、RSIが70%以上ならば…。
これらをプログラムで実現するには条件分岐のif文を使います。
if文の中には条件式を記載します。複数の条件式を記述する場合は、論理演算の論理積AND(&&)または論理和OR(||)を使って繋げます。
例えば、こんな感じです。
if(a > b && c < d){
// 処理
}
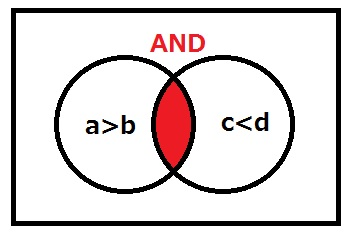
「a > b」や「c < d」が条件式ですね。通常、&&は「かつ」、||は「または」と訳します。
この場合、「aがbより大きくて、かつcがdより小さい場合に処理を実行する」という意味になります。
論理演算には他にも論理否定(!)と排他的論理和がありますが、プログラミングでは論理積、論理和、論理否定の3つで十分です。
さて、私が本記事で伝えたかったことは3つあります。
1つ目は、不等式を否定すると、不等号の向きと、不等号の種類(等号を含むか含まないか)が変わるということです。例えば、x<1の否定である「!(x<1)」は、「x>=2」になります。
2つ目は、以下のド・モルガンの法則は覚えておいて損はないということです。
- !(a && b) = (!a) || (!b)
- !(a || b) = (!a) && (!b)
3つ目は、if文内に複数の条件式が存在し、頭がこんがらがってきた場合は、ベン図を書くと頭の交通整理ができて便利ということです。
ド・モルガンの法則とベン図については、論理と集合の基本2|ド・モルガンの法則が分かりやすく解説してくれています。なお、冒頭の「共通部分,和集合,補集合の復習」は読み飛ばしても構いません。そして、集合を条件式と読み替えればOKです。
さて、1つ目と2つ目の性質を「5時~8時の早朝スキャルピング時間帯以外で何らかの処理を実行したい」という例で考えてみます。
まず、5時~8時までをif文で書くとこうなります。
if(hour >= 5 && hour <= 8){
// 処理
}
この時間帯以外(つまり否定)なので、論理否定を使います。
if(!(hour >= 5 && hour <= 8)){
// 処理
}
これでも良いですが、「!」は見落としやすいですし、パッと見わかりにくいです。
「else使えば?」という声が聞こえてきそうです。こんな感じになりますね。
if(hour >= 5 && hour <= 8){
// 何もしない
else{
// 処理
}
これもありですが、美しくないですね(たまにやっちゃいますけど)。
というわけで、論理否定のif文をド・モルガンの法則で変換してみます。
if(!(hour >= 5) || !(hour <= 8)){
// 処理
}
さらに、不等式の否定では向きと不等号の種類が変わる性質を使うと、こうなります。
if(hour < 5 || hour > 8){
// 処理
}
これならすっきりしてて見やすいです。そう思いませんか?
最初はまどろっこしく感じると思いますが、慣れてくれば素早くできるようになります。可読性を高めることはプログラムの品質を向上させることに繋がりますので、この機会にぜひマスターしましょう!